
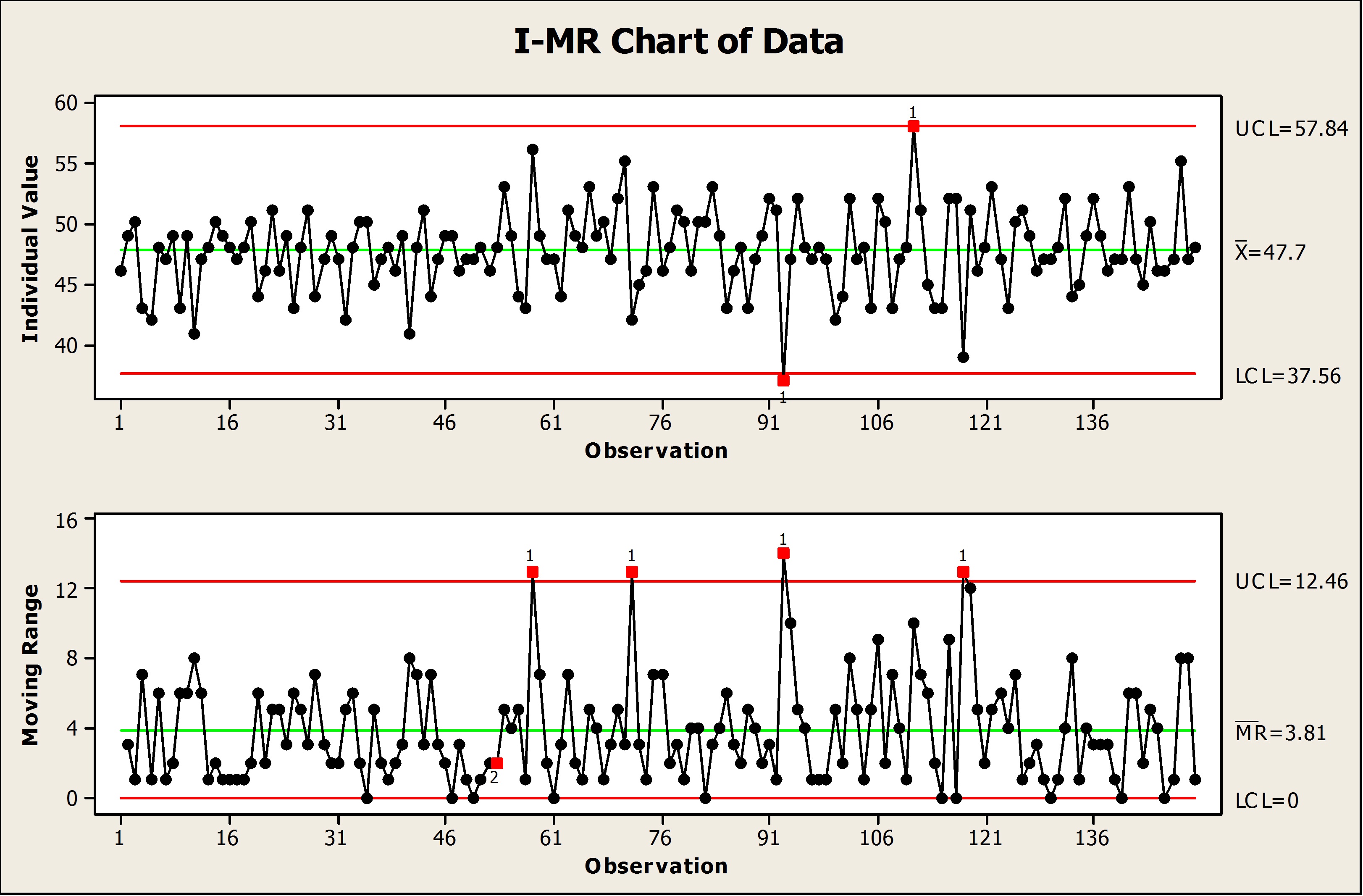
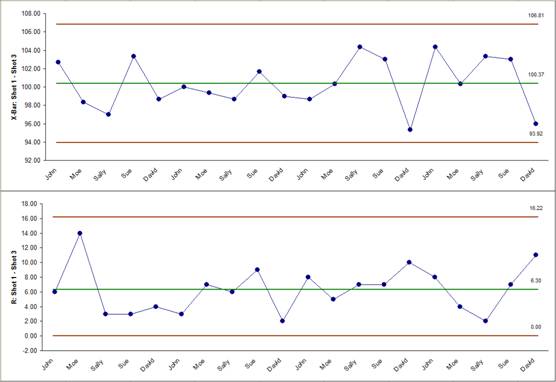
obj <- qcc(diameter, type="xbar",newdata=diameter) We can use the computed control limits for monitoring new sample data from the same process. Now, so far, we know that for nsigma=3, the process is in control. Higher confidence level means tighter control limits. You can try the same with changing confidence levels. Now 11 points are out of control, as control limits are even more tighter. obj <- qcc(diameter, type="xbar",nsigmas = 1) This is because we make control limits tighter. obj <- qcc(diameter, type="xbar",nsigmas = 2)Īs it can be seen from the plot, 3 observation points goes out of control. Let’s see what happen if I change the nsigma to 2. It can be seen from the above plots that all the 30 group observations are ” in control” If all the points lie with in the control limits, process is said to be “in control”. The main objective of control chart is to see whether a process is in “out of control”, so that appropriate action can be taken in that case. However, nsigma and confidence interval can be changed. Summary statistics show that UCL (upper controlled limit) and LCL (lower control limit) is calculated as: Centre of group statistics ± nsigma.īy default, qcc function considers nsigma= 3, means ☓ standard deviation of statistic. The summary gave the LCL (Lower Control limit) = 73.98805 and UCL (Upper control limit) =74.0143 for x-bar chart. The control chart has the center line (horizontal solid line), the upper and lower control limits (dashed lines). R chart (plotting range of all groups) and X-bar chart (plotting averages of all groups) can be created as follows: obj <- qcc(diameter, type="R") Standard Shewhart control charts can be obtained by calling qcc function. Now, we consider first 30 samples as training data. To do that we need to group the data such that each sample observation readings are in one column, so as to perform the further analysis. # loading packageīefore creating control charts, we need to create qcc object from the data, which can be done by calling qcc function. It can be seen from the data that there are total 200 observations of diameter of Piston rings- 40 samples with 5 reading/observation each.
The first step is loading the qcc package and sample data. Implementation and Interpretation of Control Charts in R Step 1 Here, we will go through qcc package (R package for statistical quality control charts) and learn “How to create control chart (to know whether the process is in control)”. There are many packages in R, which can be used for analysis related to Six Sigma. Rule 8 :- 8 consecutive points on either side of the center line with not within 1 sigma. Rule 7 :- 15 consecutive points are within 1 sigma of the center line Rule 6 :- 4 out of 5 consecutive points are more than 1 sigma from the center line in the same direction. Rule 5 :- 2 out of 3 consecutive points are more than 2 sigmas from the center line in the same direction. Rule 4 :- 14 consecutive points are alternating up and down. Rule 3 :- 6 consecutive points are steadily increasing or decreasing. Rule 2 :- 8/9 points on the same size of the center line. Rule 1 :- One or more points beyond the control limits There are 8 Control chart rules that gives the indication that there are special causes of variation :. If the control chart indicates that the process is not in control, analysis of the chart can help determine the sources of variation, as this will result in degradation of process performance. Moreover, data from the method can be used to predict the future performance of the process. If analysis of the control chart indicates that the process is currently under control, then no corrections or changes to process control parameters are needed. Control charts, also known as Shewhart charts or process-behavior charts, are a statistical process control tool used to determine if a manufacturing or business process is in a state of control. It consists of five Phases: Define, Measure, Analyse, Improve and Control.Ĭontrol charts are used during the Control phase of DMAIC methodology. Six Sigma DMAIC is the problem-solving methodology. Six Sigma is a data-driven approach and methodology for eliminating defects (driving toward six standard deviations between the mean and the nearest specification limit) in any process. Six Sigma at many organizations means a measure of quality that strives for near perfection. In this article, we will go through the implementation and interpretation of Control Charts, popularly used during Six Sigma DMAIC projects.


 0 kommentar(er)
0 kommentar(er)
